CS61A disc03 递归
edit time: 2024-07-18 20:57:12
依旧遵从disc01的案例-过程-抽象-实现的思路。
为了简化本blog及之后的blog,对于部分题目,首先会省略写出实现后、代入案例检验的过程;也可能会只取一个案例做分析,其他案例请自行思考;还可能会省略从案例抽象出某些符号的观察思考过程,直接给出实现。
在分析案例时可能会尽量将案例拆分开、遵照由简单到复杂的思考过程。如果某些步骤整合后一次性给出不易理解,可以尝试自行拆分。
还请读者自行对比思考,尽量完整理解,注意掌握分析思想。如果对理解上述思路有疑惑,可以看看本blog中讲解比较详细的题目,或者之前讲解的disc01等。
Q1: Warm Up: Recursive Multiplication
思考过程省略。
def multiply(m, n):
"""Takes two positive integers and returns their product using recursion.
>>> multiply(5, 3)
15
"""
"*** YOUR CODE HERE ***"
# Guarantee that m >= n, to simplify recursion.
if m < n:
m, n = n, m
if n == 1:
return m
else:
return m + multiply(m, n - 1)
Q2: Swipe
base: n < 10
取案例。考虑两位数的情况:eg. swipe(28)
将其转化为:一些操作,以及对降一阶(在这里就是位数少一位)的值执行swipe,一种可行操作如下:
print(8)
swipe(2)
print(8)
注意中间一定要化用位数少一位的swipe(2)函数,而不是直接print(2),这是为了构造递归,即从描述过程中取出某种抽象的、一般的物体;
在递归时,我们只考虑本情况和“相对低阶一点”的情况,而不考虑无关的情况。如题目给出的调用四位数,我们只考虑怎样将其转化为一些操作和调用三位数;或者从调用三位数考虑转化为一些操作和调用两位数。
将上述的2和8抽象为n // 10和n % 10,考虑一种实现如下:
def swipe(n):
"""Print the digits of n, one per line, first backward then forward.
>>> swipe(2837)
7
3
8
2
8
3
7
"""
if n < 10:
print(n)
else:
"*** YOUR CODE HERE ***"
print(n % 10)
swipe(n // 10)
print(n % 10)
Q3: Skip Factorial
思考省略。
def skip_factorial(n):
"""Return the product of positive integers n * (n - 2) * (n - 4) * ...
>>> skip_factorial(5) # 5 * 3 * 1
15
>>> skip_factorial(8) # 8 * 6 * 4 * 2
384
"""
if n == 1 or n == 2:
return n
else:
return n * skip_factorial(n - 2)
Q4: Recursive Hailstone
这是第一次在递归中使用返回值计数。因为比较重要,这里多写一点。
仍然从取案例开始,从案例中整理过程,从过程中抽象,从抽象到实现。
b = hailstone(1)相对更简,取该案例分析。执行时首先打印,之后它的返回值是通过return odd(1)得到的,值为1。总结出一个命题:odd(1) = 1 (1)。
再考虑稍微复杂一点:c = hailstone(2),思考经历的过程。
为了更加简化,我们可以先不考虑计数,只考虑2是怎么变成1的,以及其中经历的打印过程:
首先打印2,之后返回even(2),
而even(2)的计算过程应当为 2 // 2 得到1 ,相当于完成了与2相关的一步,
在2完成之后,要对1执行完全相同的操作,所以应当调用hailstone(1) (2)。
再考虑计数,我们利用递归的返回值而非全局变量进行计数,每执行一步返回值加一,意味着even(2)的返回值要在hailstone(1)的值基础上加一。(3)
基于以上命题(1)(2)(3),我们考虑在递归的返回值处调用相对低阶的函数。下述还把计算写到了参数中,读者当然可以在思考时拆分开,先用临时变量做计算,再将临时变量作为参数。
def hailstone(n):
"""Print out the hailstone sequence starting at n,
and return the number of elements in the sequence.
>>> a = hailstone(10)
10
5
16
8
4
2
1
>>> a
7
>>> b = hailstone(1)
1
>>> b
1
"""
print(n)
if n % 2 == 0:
return even(n)
else:
return odd(n)
def even(n):
return 1 + hailstone(n // 2)
def odd(n):
"*** YOUR CODE HERE ***"
if n == 1:
return 1
return 1 + hailstone(3 * n + 1)
Q5: Count Stair Ways
题目引导超级详细,没有其他补充。
def count_stair_ways(n):
"""Returns the number of ways to climb up a flight of
n stairs, moving either one step or two steps at a time.
>>> count_stair_ways(1)
1
>>> count_stair_ways(2)
2
>>> count_stair_ways(4)
5
"""
"*** YOUR CODE HERE ***"
if (n == 1):
return 1
elif (n == 2):
return 2
else:
return count_stair_ways(n - 1) + count_stair_ways(n - 2)
Q6: Sevens
有一个坑点:题目给的has_seven函数只实现了函数中是否含7的判断,而题目要求还要判断是否为7的倍数。
相比于从头到尾模拟,更适合这道题的可能是“取一个切面来模拟”。
首先假定读者已经搞清楚了helper function封装起来的想法:如果f(i, who, direction)的i恰好等于n,则此时的who就是我们要找的who。用下面的案例说明,我们不妨找找内层函数f返回时,各参数值为多少?
>>> sevens(6, 5)
1
>>> sevens(7, 5)
2
>>> sevens(8, 5)
1
很明显,sevens(6, 5)是f(6, 1, 1),sevens(7, 5)是f(7, 2, 1),sevens(8, 5)是f(8, 1, -1)。
以sevens(7, 5)从f(6, 1, 1)开始的思考过程为例:
此时f(6, 1, 1)这几个参数不满足i == n,所以经过“一些过程”,下次测试(即返回)f(7, 2, -1)。f(7, 2, -1)这几个参数满足i == n,返回who。
考虑上述的“一些过程”。i从6到7,who从1到2,direction从1到-1。那么我们在执行f(6, 1, 1)的过程中,who是根据当前的direction == 1来修改的,而direction却是根据新的(i + 1) == 7来修改的,务必注意。
def sevens(n, k):
"""Return the (clockwise) position of who says n among k players.
>>> sevens(2, 5)
2
>>> sevens(6, 5)
1
>>> sevens(7, 5)
2
>>> sevens(8, 5)
1
>>> sevens(9, 5)
5
>>> sevens(18, 5)
2
"""
def f(i, who, direction):
if i == n:
return who
"*** YOUR CODE HERE ***"
# change person
who = who + direction
# boundary and round
if who == (k + 1):
who = 1
elif who == 0:
who = k
# switch direction
i += 1
if has_seven(i) or ((i % 7) == 0):
direction = -direction
return f(i, who, direction)
return f(1, 1, 1)
def has_seven(n):
if n == 0:
return False
elif n % 10 == 7:
return True
else:
return has_seven(n // 10)
HW02 Q6: Count Coins
hw02懒得再开新一篇,于是写到这里了。
题目给出了一个案例:
For example, the following sets make change for 15:
- 15 1-cent coins
- 10 1-cent, 1 5-cent coins
- 5 1-cent, 2 5-cent coins
- 5 1-cent, 1 10-cent coins
- 3 5-cent coins
- 1 5-cent, 1 10-cent coin
一种树状图思路如下:
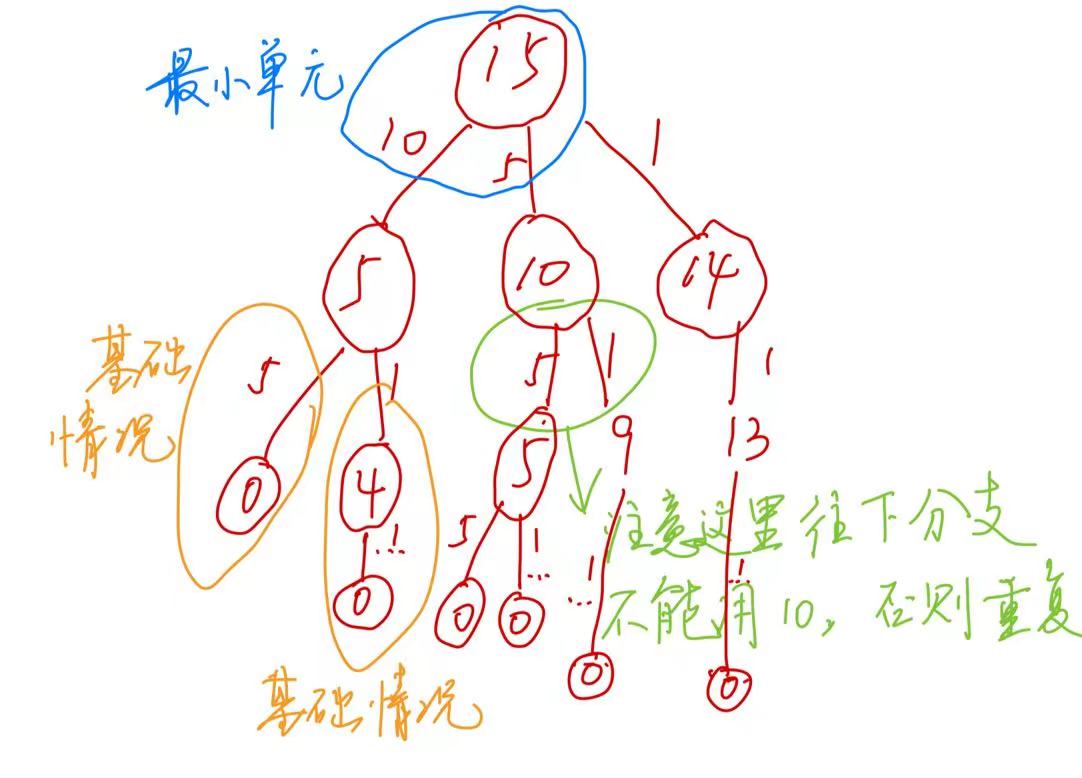
我们从上往下考虑。对于每一个金额(节点),分支上的数字是小于该金额的所有金币,并且要求下面的分支的金币面额不能大于上面的分支。则题目所示的所有情况就是从根节点(值为总金额)到叶节点(值为0)路径的总数。
观察发现以下命题 规则类怪谈 :
- 如果减到剩余的值恰为0,则计数为一。
- (可以合并到 1. 中,用于提升计算效率)如果用到的金币面额为1,仅有后面一直用面额为1的一种情况,计数为一。
- 可以把单个节点连接三个、四个及以上的分支拆解成两个分支的情况,即图中的最小单元,且这两个分支用到的金额关系是较大和较小相邻的。两个分支总共的可能性是两个分支各自的可能性之和。
从而可能的方法如下:
(以下Solution1 和 Solution 1 another implement都能跑,至于Solution 2, 3, 4, ..., 114514就交给你啦())
# Solution 1
# def helper(remain, coin):
# if coin == None:
# return 0
# if remain == 0:
# return 1 # Sum up to total.
# elif (coin > remain):
# return helper(remain, next_smaller_coin(coin))
# else:
# return helper(remain - coin, coin) + helper(remain, next_smaller_coin(coin))
# Solution 1 another implement
def helper(remain, coin):
if coin == 1:
return 1
if remain == 0:
return 1
elif remain < 0:
return 0
else:
return helper(remain - coin, coin) + helper(remain, next_smaller_coin(coin))
return helper(remain = total, coin = 25)
当然,如果认真听了课,学会了 count_partition 那道更一般的情况,这一道题也是相似的。最终要总结出类似于以下这样的命题:
- In
count_partitionsfrom lecture, the recursive case is to partitionn-musing parts up to sizemand to partitionnusing parts up to sizem-1. (引自 Discussion 4 | CS 61A Summer 2024 )