十派的玩具箱

存着各种各样的不明物体

首页 CS相关 标签们 自设 友链

CSAPP: cachelab

2024-06-05 16 min read # CSAPP

man, what can I say.jpg

Cachelab

python2 driver.py

phase1

一开始错理解为只有S指令时才保存cache，忽略了cache本来就是为了访问，所以只要有访问就应该保存cache。将这一点修改之后问题就迎刃而解了。

phase2

./test-trans -M 32 -N 32

上述指令遇到了

Function 0 (2 total)
Step 1: Validating and generating memory traces
sh: 1: valgrind: not found
Validation error at function 126! Run ./tracegen -M 32 -N 32 -F 0 for details.
Skipping performance evaluation for this function.

这样的问题，排查确认是未安装valgrind，利用sudo apt install valgrind 就解决了。

32 * 32: 关于分块利用局部性的分析

缓存大小

由于程序中static A, B 部分的相关定义~~（静态链接）~~，可以认为A、B地址连续（中间无填充），它们对应的Cache的组和行的分布恰好是完全相同的（见下图）（这会造成对角线一定的Conflict Miss，见下）。

缓存的利用机制如下：

给出的s = 5, E = 1, b = 5 计算可知对应的Cache大小为2^5 * 1 * 2^5 = 1024 Bytes。考虑到int类型为4 Bytes，

我们对A和B使用的Cache有S = 2^s = 2^5 = 32组，每组有E = 1行，每行存储了8 int的块。

不妨把这些组的唯一行编号为Line 00 到Line 31，见下图。

缓存过程分析：为什么要分块？

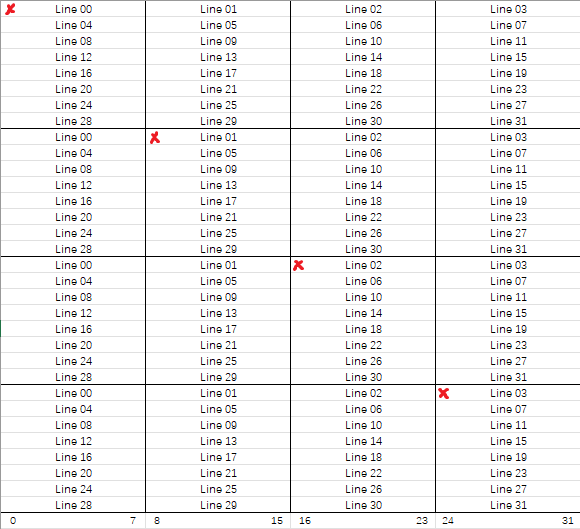
这个图是我自己画的。形式参考自：CSAPP - Cache Lab的更(最)优秀的解法 - 知乎 (zhihu.com)，非常感谢原作者的优秀思考。

从开头举例，原始转置操作B[j][i] = A[i][j]指令经历了如下的过程：

读A[0][0]，Line 00中无该值，发生Cold Miss，将A[0][0]到A[0][7] 存入Line 00中。

写B[0][0]，Line 00中无该值，且该行恰好存了A[0][0]到A[0][7] ，发生Conflict Miss和Eviction，Line 00换为B[0][0]到B[0][7]。（注意取出B时是行优先，虽然B是按列写的，但我们存入缓存是按内存连续、即按行存的，这是课本中提到的最重要的局部性问题的来源）

读A[0][1]，Line 00中无该值（上述已Eviction），发生Conflict Miss，将A[0][0]到A[0][7] 存入Line 00中。

写B[1][0]，Line 04中无该值，发生Cold Miss，将B[1][0]到B[1][7]存入Line 04中。

读A[0][2]，Line 00中有该值，发生hit。

写B[2][0]，Line 08中无该值，将B[2][0]到B[2][7]存入Line 08中。

读A[0][3]，Line 00中有该值，发生hit。

写B[3][0]，Line 12中无该值，将B[3][0]到B[3][7]存入Line 12中。

读A[0][4]，Line 00中有该值，发生hit。

写B[4][0]，Line 16中无该值，将B[4][0]到B[4][7]存入Line 16中。

...

读A[0][8]，Line 01中无该值，发生Cold Miss，将A[0][8]到A[0][15] 存入Line 01中。

写B[8][0]，Line 00中无该值，发生Conflict Miss，将B[8][0]到B[8][7]存入Line 00中。

...

为了便于理解，我详细阐述了整个过程。利用我们小学或者幼儿园学到的找规律可以知道：

  1. A[i][i]和B[i][i]会引起Conflict Miss。具体而言，写B[i][i]时会驱逐相同的Cache Line，导致A[i][i + 1]冲突不命中。（由于i = 0, 1, ..., 31，共计32次miss）（其实此处分析不完全，见下述第二次改进）
  2. A具有良好的局部性，只在每读入8个int的第一个才会发生Cold Miss，其余都是Hit。（共计128次miss）
  3. B的缓存未良好使用，每次写入都会发生Miss。（共计1024次miss）。

求和即miss总次数为32 + 128 + 1024 - 4（上述1. 与 2.在图中标红处共计4次重复计数） = 1180。

查询源码可以发现valgrind本身使用了3次miss，即得下述Function 1的misses:1183。

第一次改进：使用8 * 8分块

我们在理解了为什么会发生冲突之后，分块的作用就显而易见了。

首先利用分块解决影响最大的问题：B按列读取，每读入8块时即驱逐之前的缓存。为了解决这个问题，我们可以考虑 8×88 \times 8​的分块，在下一次驱逐缓存行之前先完成所有缓存行的传入。

void transpose_submit(int M, int N, int A[N][M], int B[M][N])
{
    int i, j, a, b, c, d, e, f, g, h;
    for (i = 0; i < N; i+=8) {
        for (j = 0; j < M; j+=8) {
            // 8 * 8
            for (int ii = i; ii < i + 8; ii++) {
                for (int jj = j; jj < j + 8; jj++) {
                    B[jj][ii] = A[ii][jj];
                }
            }
        }
    }
}

得到的结果如下Function 0：

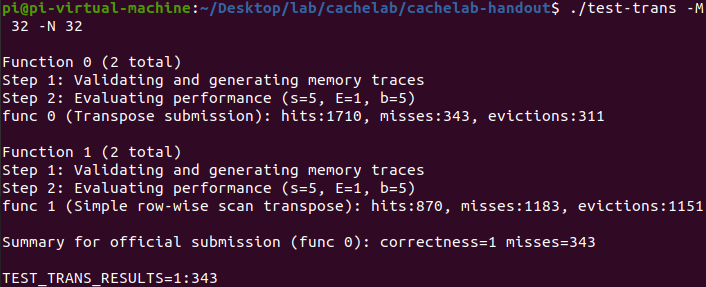
相比于原始代码Function 1，已经有了极大改善。

第二次改进：使用局部变量

之后继续修改，处理对角的conflict miss。

我们在之前“可以认为”那里发现，如果我们要从A[i][j]转置到B[i][j]即转置相同坐标的元素，会必定驱逐相同的Cache Line，造成冲突不命中。那么什么时候会转置到相同坐标位置呢？显而易见，方阵对角线处，即i == j。

但是我们按照前述计算的理论值应当为 32 + 128 + 128 = 288次，与340次（显示值misses = 343）仍然相差一定数值，说明我们的分析仍然有问题。这是为什么？

我们不妨重新仔细分析 8 * 8 分块后A和B分别使用的Cache Line。对于A使用的(x, y) (x, y = 0, 1, 2, 3)块，它对应与B使用的(y, x)块，我们会发现除了x == y的其他情况的对应块所包含的Cache Line都不重合。因此我们大胆猜测，造成这一部分问题的是对角块冲突，而非对角线元素冲突。

当前转置操作经历了如下的过程：

读A[0][0]，Line 00中无该值，发生Cold Miss，将A[0][0]到A[0][7] 存入Line 00中。

写B[0][0]，Line 00中无该值，且该行恰好存了A[0][0]到A[0][7] ，发生Conflict Miss和Eviction，Line 00换为B[0][0]到B[0][7]。

读A[0][1]，Line 00中无该值（上述已Eviction），发生Conflict Miss，将A[0][0]到A[0][7] 存入Line 00中。(1)

写B[1][0]，Line 04中无该值，发生Cold Miss，将B[1][0]到B[1][7]存入Line 04中。

读A[0][2]，Line 00中有该值，发生hit。

...

读A[1][0]，Line 04中无该值，miss，Line 04 := A[1][0..7]

写B[0][1]，Line 00中无该值，miss，Line 00 := B[0][0..7] (2)

读A[1][1]，Line 04中有该值，hit

写B[1][1]，Line 04中无该值，miss，Line 04 := B[1][0..7] (3)

我们发现之前分析到的对角线元素、即A和B同一坐标处使用相同行存取的影响分为三部分：

  1. A[i][i + 1]处出现Conflict Miss （上述标号**(1)**），这是因为写B[i][i]时驱逐了A[i][i + 1]本应被缓存到的行。
  2. B[i][i + 1]处出现Conflict Miss（上述标号**(2)**），这是因为写B[i][i + 1]时本应使用上一部分提到的写B[i][i]缓存的行，但它被上一部分读A[i][i + 1]时驱逐了。
  3. B[i][i]处出现Conflict Miss（上述标号**(3)**），这是因为我们在写B[i][i]之前一定会先读A[i][i]导致驱逐。

上述1、2可以归类为对角块冲突造成的影响 相爱相杀 ，而3可以归类为对角线元素冲突造成的影响。

由这三部分影响、连同无法避免的Cold Miss造成的所有miss对应A、B矩阵见下两图：


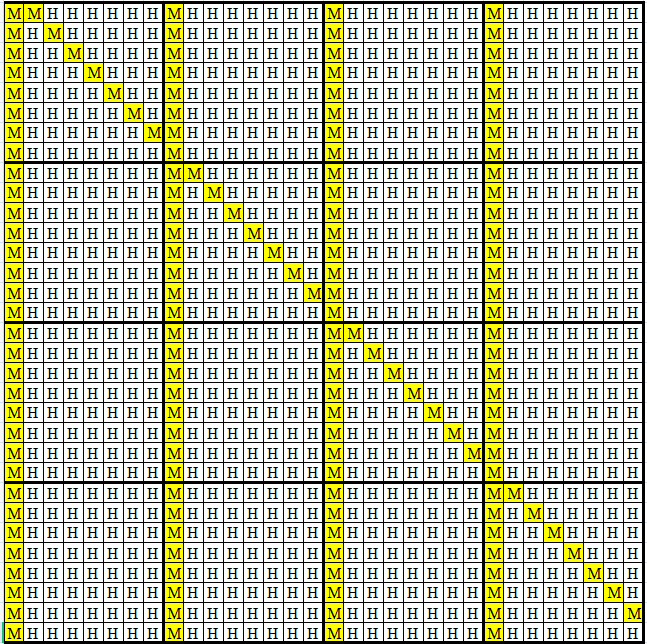
图片来源：CSAPP - CacheLab (d-sketon.top)

为了规避上述由对角块造成的1、2问题，我们考虑利用题目所给的共计12个局部变量。对于每一个 8 * 8 分块，可以将A[i][i..(i + 7)]存入8个临时变量中，利用临时变量而非Cache进行转置。

这样虽然似乎与Cache本身的意义有少许矛盾（甚至有种开挂感），但就优化而言是可行的。优化理论结果 misses = 128 + 128 + 32 = 288。同上-4即得284，与下图（显示值misses = 287）符合。

void transpose_submit(int M, int N, int A[N][M], int B[M][N])
{
    int i, j, a, b, c, d, e, f, g, h, k;
    for (i = 0; i < N; i+=8) {
        for (j = 0; j < M; j+=8) {
            // copy the A(i, j) block, row by row. Then paste it to B(j, i).
            for (int k = 0; k < 8; k++) {
                a = A[i + k][j];
                b = A[i + k][j + 1];
                c = A[i + k][j + 2];
                d = A[i + k][j + 3];
                e = A[i + k][j + 4];
                f = A[i + k][j + 5];
                g = A[i + k][j + 6];
                h = A[i + k][j + 7];
                B[j][i + k] = a;
                B[j + 1][i + k] = b;
                B[j + 2][i + k] = c;
                B[j + 3][i + k] = d;
                B[j + 4][i + k] = e;
                B[j + 5][i + k] = f;
                B[j + 6][i + k] = g;
                B[j + 7][i + k] = h;
            }
        }
    }
}

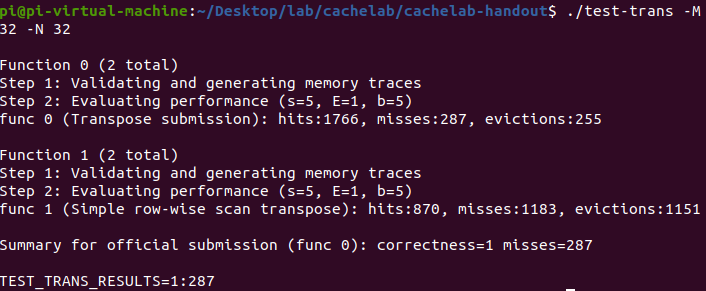
64 * 64

有了上述分析，本次只需多尝试不同的分块方法、再思考做优化即迎刃而解了。

区块用到的组

图片来源：CSAPP - Cache Lab的更(最)优秀的解法 - 知乎 (zhihu.com)，虽然之前感谢过一次了，但再次感谢原作者的优秀思考。

看图发现 8 * 8 的分块内部上下两部分存在冲突，所以考虑继续缩小分块，先用 4 * 4分块尝试：

    if (M == 64) {
        for (int i = 0; i < N; i += 4) {
            for (int j = 0; j < M; j += 4) {
                // copy the A(i, j) block, row by row. Then paste it to B(j, i).
                for (int k = 0; k < 4; k++) {
                    a = A[i + k][j];
                    b = A[i + k][j + 1];
                    c = A[i + k][j + 2];
                    d = A[i + k][j + 3];
                    B[j][i + k] = a;
                    B[j + 1][i + k] = b;
                    B[j + 2][i + k] = c;
                    B[j + 3][i + k] = d;
                }
            }
        }
    }

结果如下：

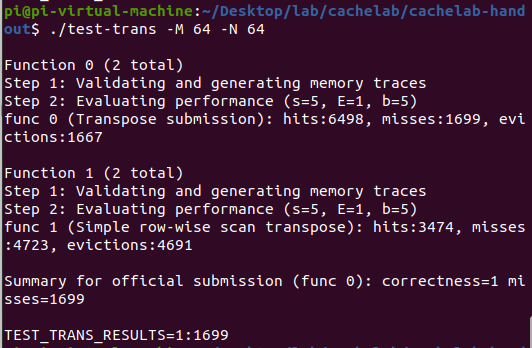
结果未达到1300以下，考虑继续优化。

是否可以利用 4 * 8 的分块呢？4 * 8的分块内部的确不存在冲突，可以充分利用A的局部性，但置于B之后就不可以了。由此我们思考：是否可以先将A的 4 * 8 块置于B的相同位置、再将其中不在对角线上、需要转置的4 * 4块转置过来，如是操作，以相比于上述 4 * 4 分块的方式更好利用A的局部性？

代码如下：

if (M == 64) {
        for (int i = 0; i < N; i += 8) {
            for (int j = 0; j < M; j += 8) {
                
                for (int k = i; k < i + 4; k++) {
                    // copy the A(i, j) 4 * 8 block(4 * 4 block 1, 2), row by row.
                    // Then paste it to B(i, j).
                    // So block1 is at the right place,
                    // block2 should be transposed.
                    a = A[k][j];
                    b = A[k][j + 1];
                    c = A[k][j + 2];
                    d = A[k][j + 3];
                    e = A[k][j + 4];
                    f = A[k][j + 5];
                    g = A[k][j + 6];
                    h = A[k][j + 7];
                    B[j][k] = a;
                    B[j + 1][k] = b;
                    B[j + 2][k] = c;
                    B[j + 3][k] = d;
                    B[j + 0][k + 4] = e;
                    B[j + 1][k + 4] = f;
                    B[j + 2][k + 4] = g;
                    B[j + 3][k + 4] = h;
                }

                for (int k = j; k < j + 4; k++) {
                    // Store block2, row by row.
                    a = B[k][i + 4];
                    b = B[k][i + 5];
                    c = B[k][i + 6];
                    d = B[k][i + 7];
                    // Store block3 in A.
                    e = A[i + 4][k];
                    f = A[i + 5][k];
                    g = A[i + 6][k];
                    h = A[i + 7][k];
                    // Copy block3 to the place of block2(transpose block3).
                    B[k][i + 4] = e;
                    B[k][i + 5] = f;
                    B[k][i + 6] = g;
                    B[k][i + 7] = h;
                    // Copy block2 to the place of block3(transpose block2).
                    B[k + 4][i] = a;
                    B[k + 4][i + 1] = b;
                    B[k + 4][i + 2] = c;
                    B[k + 4][i + 3] = d;
                }

                for (int k = i + 4; k < i + 8; k++) {
                    // Copy block4.
                    a = A[k][j + 4];
                    b = A[k][j + 5];
                    c = A[k][j + 6];
                    d = A[k][j + 7];
                    B[j + 4][k] = a;
                    B[j + 5][k] = b;
                    B[j + 6][k] = c;
                    B[j + 7][k] = d;
                }
            }
        }
    }

结果如下：

61 * 67

尝试对大部分块使用 8 * 8 分块，对边界处的直接转置，

    if (M == 61) {
        for (int i = 0; i < N; i += 8) {
            for (int j = 0; j < M; j += 8) {
                // Solve the boundary. Use 8 * 8 block for most places.
                if (i + 8 <= N && j + 8 <= M) {
                    // copy the A(i, j) block, row by row. Then paste it to B(j, i).
                    for (int k = i; k < i + 8; k++) {
                        a = A[k][j];
                        b = A[k][j + 1];
                        c = A[k][j + 2];
                        d = A[k][j + 3];
                        e = A[k][j + 4];
                        f = A[k][j + 5];
                        g = A[k][j + 6];
                        h = A[k][j + 7];
                        B[j][k] = a;
                        B[j + 1][k] = b;
                        B[j + 2][k] = c;
                        B[j + 3][k] = d;
                        B[j + 4][k] = e;
                        B[j + 5][k] = f;
                        B[j + 6][k] = g;
                        B[j + 7][k] = h;
                    }
                }
                else {
                    // For the boundary, transpose directly.
                    // k < min(i + 8, N), s < min(j + 8, M)
                    for (int k = i; k < (((i + 8) < N) ? (i + 8) : N); k++) {
                        for (int l = j; l < (((j + 8) < M) ? (j + 8) : M); l++) {
                            B[l][k] = A[k][l];
                        }
                    }
                    
                }

            }
        }
    }

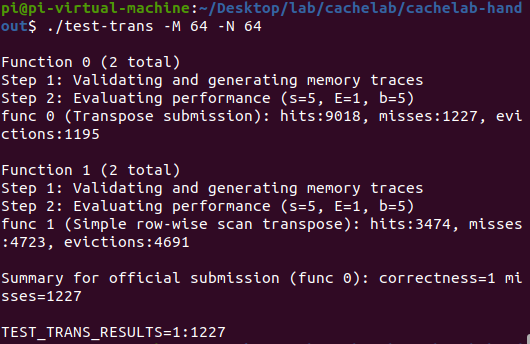
结果如下：

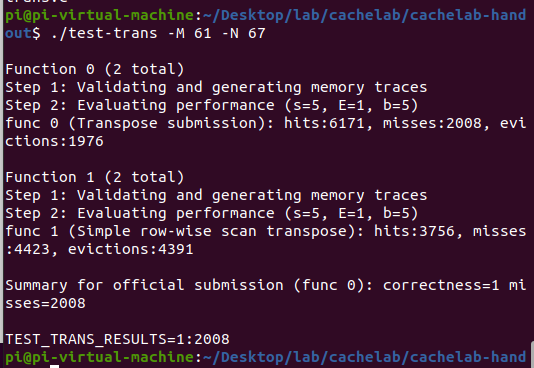
正好不在2000以下。

思考我们的分块之后，决定把长边设置为循环变量，重新测试：

    if (M == 61) {
        for (int i = 0; i < N; i += 8) {
            for (int j = 0; j < M; j += 8) {
                // Solve the boundary. Use 8 * 8 block for most places.
                if (i + 8 <= N && j + 8 <= M) {
                    // copy the A(i, j) block, row by row. Then paste it to B(j, i).
                    for (int k = j; k < j + 8; k++) {
                        a = A[i][k];
                        b = A[i + 1][k];
                        c = A[i + 2][k];
                        d = A[i + 3][k];
                        e = A[i + 4][k];
                        f = A[i + 5][k];
                        g = A[i + 6][k];
                        h = A[i + 7][k];
                        B[k][i] = a;
                        B[k][i + 1] = b;
                        B[k][i + 2] = c;
                        B[k][i + 3] = d;
                        B[k][i + 4] = e;
                        B[k][i + 5] = f;
                        B[k][i + 6] = g;
                        B[k][i + 7] = h;
                    }
                }
                else {
                    // For the boundary, transpose directly.
                    // k < min(i + 8, N), s < min(j + 8, M)
                    for (int k = i; k < (((i + 8) < N) ? (i + 8) : N); k++) {
                        for (int l = j; l < (((j + 8) < M) ? (j + 8) : M); l++) {
                            B[l][k] = A[k][l];
                        }
                    }
                    
                }

            }
        }
    }

结果如下：

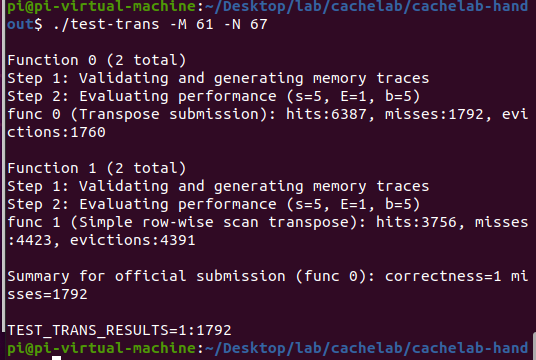
成功通过。

Powered by Gridea RSS