十派的玩具箱

存着各种各样的不明物体

首页 CS相关 标签们 自设 友链

CSAPP: datalab

2024-04-30 12 min read # CSAPP

最近没写什么其他好玩的东西，拿课堂作业报告水一水blog。

运行结果

dlc

make
./dlc -e bits.c

btest

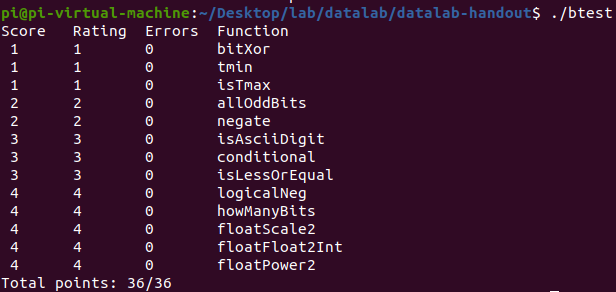
./btest

思路

bitXor

  • 解法一

直接考虑所求的两种情况。

利用对称差公式：x ^ y = (x&~y) | (y&~x)，

我们需要取这两种情况，所以取两次反，

并将其中一次取反运用于狄·摩根律完成从|到&的转换，即得所求为

~(~(x & ~y) & ~(y & ~x))。

  • 解法二

考虑反面的另外两种情况。

x和y均为1或0时，x^y返回0。单独取这两种情况即为 (x & y) | (~x & ~y)。

取其反面即为~( (x & y) | (~x & ~y) )。

再运用狄·摩根律：~(a|b)=(~a)&(~b) 完成从|到&的转换，即得所求为

~(~(x & y)) & ~(~x & ~y))。

tmin

32位的Two's complement范围为 −231-2^{31}到231−12^{31}-1，

其中Tmin=−231=(1<<31)T_{min}=-2^{31}=(1<<31)，即为首位为1、其余全0。

isTmax

Tmax=231−1T_{max}=2^{31}-1，即为首位为0、其余全1，

  1. 正常思路是比较其取反是否为TminT_{min}，即返回值为 ~Tmax == Tmin。

但本题中不允许使用左移，也不能直接构造Tmin = 0x80000000，

所以TminT_{min}要通过Tmax+1T_{max}+1得到，即~x == x + 1。

根据课本习题，a==b可以表示为 !(a^b) （因为a是自身的加法逆元，a^a=0，取非!即得1），

符合题目中返回值只有1和0的条件。所以返回值改写为!(~x ^ (x + 1))。

  1. 但根据数据验证，发现-1也满足上述条件~x == x + 1，所以将-1另外排除，即正常思路为x != -1。

再根据符号限制得到条件为!!(x + 1)。

（用两次!是因为最终使用位与验证1、2条件同时满足，所以两个条件的值应该为0或1。但x+1的值不一定为0或1，所以用!规格化可以使其他非-1的值全部返回0，符合我们的需求）

综上得到返回值为 !(~x ^ (x + 1)) & !!(x + 1)，共8 ops，

为了再简化可以反用前述狄摩根律写为!((~x ^ (x + 1)) | !((x + 1) ^ 0))，共7 ops。

allOddBits

因为所给符号与位数关联的只有左右移，需要人为构造，

考虑使用掩码(BitMask)，即x & BitMask某一位为1当且仅当x和BitMask该位同时为1。

由于允许使用的常数范围为0x000x00到0xFF0xFF​，首先考虑长为8 bits的奇数x位置为1，相应掩码为[1010 1010]即int bitMask = 0xAA。其满足的条件应为 x & bitMask == bitMask，即!((x & bitMask) ^ 0xbitMask)。

如果对x的所有8 Byte均判断，结果需要大量符号，所以构造所需的32 bits掩码即可。即

int bitMask = (0xAA << 24) | (0xAA << 16) | (0xAA << 8) | 0xAA。

negate

根据课本对模数加法构成阿贝尔群的论述，Tmin的加法逆元为Tmin，而其他数x的加法逆元为-x。

这两种结果都满足 -x == ~x + 1 。

isAsciiDigit

题目需要人为构造，考虑使用掩码。

考虑题设条件：[0011 0000] <= x <= [0011 1001]，可以用以下条件逐位判断：

if ((x >> 4) == 0x3) {
	int 3rdBit = (x >> 3) & 0x1; // the 3rd bit, counting from 0th
	if (3rdBit == 0) return 1;
	else {
		// if 3rdBit == 1, then 2ndBit and 1stBit must be [00]
		int 2ndAnd1stBit = (x >> 1) & 0x3;
		if (2rdAnd1stBit == 0) return 1;
		else return 0;
	}
}
else return 0;

接下来将上述条件简化并根据所给符号改写即可，改写举例如下：

int HigherByteCond = !((x >> 4) ^ 0x3);
int the3rdBit = (x >> 3) & 0x1;
int the2ndAnd1stBit = (x >> 1) & 0x3;
return HigherByteCond & ((!the3rdBit) | (the3rdBit & (!the2ndAnd1stBit)));

共计12 ops。

conditional

首先考虑没有限制的情况，再根据限制改写符号。

不考虑符号时如下：

if (x) return z;
else return y;

因为z和y具有某种程度的对称性，返回z可以拆成z + 0，返回y可以拆成 0 + y，

所以如果按照python的逻辑与，返回值可以写为(cond && z) | (!cond && y)或(cond && z) + (!cond && y)。（python中，逻辑与的两侧如果同时非0，则返回其右侧的值）

但需要考虑多位的返回值时，&&不能简单地改写为位与，所以另寻他法，即掩码运算。

因为x只有非0和0，所以一定需要首先使用int cond = !x;来规格化，从而只考虑条件值为1和0的情况。

如果z和y均只有一位，则返回值可以写为 cond & z + (!cond) & y，注意到cond实际扮演了掩码的角色。这为我们提供了灵感：可以根据cond构造所需长度的掩码（0xFFFFFFFF和0x00000000），规避显式的条件判断。即所需返回值为 bitMask & z + ~bitMask & y，只需构造bitMask即可。

最后注意到取负可以分别将cond为1和0时映射到0xFFFFFFFF即-1与0x00000000即0，完成bitMask的构造。

综上，本题思路如下：

int cond = !x;
int bitMask = ~cond + 1;
return ((~bitMask) & y) + (bitMask & z);

isLessOrEqual

用差实现比较，差通过取负实现。

根据课本，作和差时需要考虑溢出问题。正溢出得负数，负溢出得正数，判断即可。

同号则一定不溢出、返回diffSign；前0后1时返回0、前1后0时返回1，即返回xSign。

注意diffSign最好使用-x + y得到，它的符号位在x <= y时一定为0，反之一定为1；

而如果使用x + (-y)就不会有这样良好的效果（当x == y时）。

int xSign = (x >> 31) & 0x1;
int ySign = (y >> 31) & 0x1;
int signXor = xSign ^ ySign;
int negaX = ~x + 1; 
int diffSign = ((negaX + y) >> 31) & 0x1;
return ((!signXor) & (!diffSign)) | (signXor & xSign);

logicalNeg

能够区分0和非0的性质非常有限，比如x == -x。但如果异或两个完整值，则仍然没有规避规格化问题。

  • 解法一

考虑判断x与-x的符号位，并只对这一位做异或得到signXor，

再将得到的0映射到1，得到的1映射到0即可，可以返回1 - signXor = 2 + ~(signXor)。

除此之外，之前提到了Tmin的加法逆元也是其本身，需要排除掉。

int signXor = ((x ^ (~x + 1)) >> 31) & 0x1;
return ~(x >> 31) & (2 + ~(signXor));

将0映射到1、将1映射到0也可以通过“加法逆元”即与1异或实现，即返回signXor ^ 0x1。

int signXor = ((x ^ (~x + 1)) >> 31) & 0x1;
return ~(x >> 31) & (signXor ^ 0x1);

共计9 ops。

  • 解法二

相比于异或，先“并”再移位之后取反得到的符号判断可以将Tmin也包含在非0的情况中，省去返回值的特判。

int sameSign = ((x | (~x + 1)) >> 31) & 0x1;
return sameSign ^ 0x1;

甚至只有6 ops。

howManyBits

好难，需要多次细分。

首先要注意这道题并没有限制字长为32，所以可以只用符号位的1 bit表示-1。

正因如此，获得了重要的对称性：某个负值表示需要的比特数恰好等同于其取反需要的比特数，

所以利用掩码将负值取反得到正值，正值或0不变：

掩码取x >> 31，类似于前述conditional，置y=x, z=~x。

之后利用二分思想，将判断区间划分为16、8、4、2、1。

这基于以下事实：如果高16位不全为0（!!(x >> 16) == 1），则低16位需要被表示出来，即答案加16。

同理，如果 !!(x >> power) == 1，则答案加power=2m=(1<<m)power=2^m=(1 << m)，

即加 bPower = !!(x >> power) << m。

其中写作powerpower而非1 << m是为了节省符号数。分别取power=16,8,4,2,1,0power=16,8,4,2,1,0判断、再将x右移bPower位即可。

floatScale2

终于解锁了条件判断和大常数。首先将浮点数拆分得到s, exp, frac分别占1, 8, 23位。

特判NaN情况，除此之外：

如果为非规格化（exp == 0），则直接给frac左移一位（注意使用位或的原因：当frac最高位为1时，这样的左移恰好为exp提供1，使其转化为较连续的非规格化值）；

如果为规格化 （exp != 0 && exp != 0xFF），则给exp加一。

floatFloat2Int

特判：exp == 0xFF 时返回 0x80000000u即1<<31。

其他情况不妨首先考虑非负数情况，如果为负数则在最后取负。

非规格化：exp == 0，其表示值范围为 0≤x<10 \le x < 1，强制类型转换为int则直接向0取整返回0。可以合并到下述E<0的情况。

规格化：V=(−1)s×M×2EV=(-1)^s \times M \times 2^E，其中E=e−Bias=e−127E=e-Bias=e-127。

当E<0时，V<1V<1，直接返回0；

当E>=31时，V>Tmax=231−1V>Tmax=2^{31}-1，特判返回0x80000000u即1<<31。

接下来处理其他情况。

在相乘之前给M补回隐含的1，即 frac |= 0x800000;，则包含一开始的掩码操作在内，我们此时取得的unsigned frac 是一个以1开头的24位的unsigned，相当于已经给规格化公式所需的值M(1 <= M < 2) 左移了23位。

即当E >= 24时，我们已左移的23位还需继续左移，即再左移E - 23位，总共左移了E位，满足M×2EM \times 2^E，

当E <= 23时，我们将已左移的23位回退23 - E位，相当于实际左移了E位，满足M×2EM \times 2^E。

最后根据符号s返回相应正负值即可。

floatPower2

要注意到答案2x2^x的值一定大于0，则它能取到的最小值是非规格化数表示的最小正值，最大值是规格化数表示的最大正值。

先考虑非规格化数。考虑除0之外最小的非规格化数，即E=1−127=−126E=1-127=-126，frac=2−23frac=2^{-23}， 此时V=2−126×2−23=2−149V=2^{-126} \times 2^{-23}=2^{-149}即为可以表示的最小值。因此如果x < -149，则精度太高、无法表示，直接返回0。

其余非规格化数的情况在精度范围内，frac = x + 149，此时要表示成float串，只有frac部分，表示的值恰好为实际值VV，$V=2^{-126} \times 2^{-23} \times 2x=2{x-149} $，故返回 1 << (x + 149) 。直到左移至exp不为0，所以这种情况的边界条件是 x <= -127。

当x + 149 >= 23即x >= -126时，开始规格化表示。对于规格化数，能表示的最大数的数量级应为exp除了第一位以外全为1、即exp==127，因此当x > 127时返回+INF即0xFF << 23。

其余规格化数的情况是-126 <= x <= 127，此时要表示成float串，e = E + 127 = x + 127，而frac部分均为0，即返回(x + 127) << 23。

Powered by Gridea RSS