十派的玩具箱

edit time: 2025-06-17 01:43:17
ps. 以下所有例子里的s都取0，即我们考虑的是正数和正0的浮点表示。
s取1就是给正数前面添个负号。
以下未引入由于精度带来舍入问题的例子。

十进制数转浮点数、浮点数转十进制数步骤

十进制数转浮点数步骤：

1. 十进制转二进制，如$10.001_{2}$。
2. 二进制转二进制的科学计数法表示（$1.xxx_2 \times 2^{yyy}$），如$1.001_{2} \times 2^1$，根据指数$yyy$参考下述“规格化和非规格化判断”。
3. 根据二进制的科学计数法表示，参考下述“M和E是多少”，写出s, exp, frac。

浮点数转十进制数步骤：反过来
根据exp判断为规格化、非规格化、无穷大、NaN中的哪一种，
如果为规格化和非规格化，则将exp和frac按照对应规则转化为E和M，
进而得到表示的数 $V=(-1)^s \times M \times 2^E$。

规格化和非规格化判断

省流：看要表示的数的二进制科学计数法的指数是否在规格化可提供的E范围内。

以s, exp, frac三个二进制段长度为1, 4, 3为例：
根据浮点数表示给出的exp段长度k=4，可以得到$Bias = 2^{k - 1} - 1=7$。
非规格化数是形如 0 0000 xxx 等的形式，即中间exp段全0。
规格化数是形如 0 0011 xxx 等的形式，即中间exp段既不全0、也不全1。
无穷大是 0 1111 000，即中间exp段全1且frac段全0。
NaN是 0 1111 xxx（xxx≠000），即中间exp段全1且frac段不为全0。

由规格化数的定义可以推得：
最小的规格化数为 0 0001 000，即exp为0001。
最大的规格化数为 0 1110 111，即exp为1110。
ps. 可以记住：右边的frac从000到111对应的数逐渐增大，从而推得最小和最大的规格化数。

对于规格化数，满足$E = exp - Bias$，
所以最小的规格化数对应的E=1-7=-6（0001对应1），
最大的规格化数对应的E=14-7=7（1110对应14）。
关键：
要表示的数的二进制科学计数法的指数在规格化能提供的$[-6, 7]$范围内，就一律为规格化数。
如果指数小于-6，则为非规格化数。
如果指数大于7，则为无穷大。

M和E是多少

省流：
根据判断出的是规格化还是非规格化，
把二进制的科学计数法表示的小数部分和指数部分套进对应的规则。

eg. 下面表示里s, exp, frac三个二进制段长度为1, 4, 3

总结：还是以这个例子为例，
要表示的数的二进制科学计数法的指数在规格化能提供的$[-6, 7]$范围内，就一律为规格化数，E即为指数，M=$1.xxx_2$。
如果指数小于-6，则为非规格化数，E取-6，把科学计数法表示拆成 $1.xxx_2 \times 2^{yyy-E} \times 2^{E}$ 的形式。M=$1.xxx_2 \times 2^{yyy-E}$，从而M是$0.zzz$的形式，以表示更小的指数。如果指数实在太小（见备注），则直接用0表示。
如果指数大于7，则用无穷大表示，不需要E和M。

在根据要表示的数的二进制科学计数法得到M和E之后，就能得到exp和frac字段：

1. M和frac字段
   非规格化数frac字段对应的$M$是 0.frac，即0.连上frac部分。
   eg. 0 0000 010对应的小数是$0.010_{2}$ * 2^(-6) （为什么是-6后面说）
   规格化数frac字段对应的M是 1.frac，即1.连上frac部分。
   eg. 0 0111 001对应的小数是$1.001_2$ * 2^0（为什么是0后面说）

2. E和exp字段
   非规格化数，exp字段对应的E是1-Bias。
   eg. 0 0000 010对应的Bias是2^(4-1)-1=7（exp长度为4），E=1-7=-6，故对应的小数是0.010 * 2^(-6)
   规格化数，exp字段对应的E是exp-Bias。
   eg. 0 0111 001对应的Bias是2^(4-1)-1=7（exp长度为4），E=exp-Bias=7-7=0，故对应的小数是1.001 * 2^0。

注意exp和frac字段补0的方式不同，就像是它们之间有一个小数点一样。
exp是往前补0，比如$10_2$补0变成$0010$，
frac是往后补0，比如$01_2$补0变成$010$。

备注. “指数实在太小”是多小？
最小的非规格化数，上例即0 0000 001，此时E=1-7=-6，M=$0.001_2=2^{-3}$，这个数是$2^{-9}$。
如果再小一些、且不能舍入到最小的非规格化数，就只能舍入到0 0000 000即0了。

例题

以下例子不小心只有规格化和NaN，非规格化、指数太大、指数太小再找点例子练练。

例题1：十进制转换为浮点表示。将0.625转换为浮点数表示，s, exp, frac分别为1, 4, 3位。

0. 顺手算一下Bias = 2^(k - 1) - 1 = 2^(4-1)-1=7，其中k是exp的位数。
1. 十转二，整数除二看余、小数乘二看整。0.625乘二、乘二、乘二得到的整数分别为1、0、1，故它的二进制表示是0.101。
2. 转换为1.xxx的形式，即1.01 ^ 2(-1)。
3. 对应到V的式子上，M=1.01，E=-1。因为E大于规格化数表示中最小的E（exp值为1、E=exp-Bias=1-7=-6），所以这个数按照规格化表示。
4. 规格化表示的frac直接写M舍去1和小数点、后面的一段（M=1.01 -> frac表示为010，注意根据位数往后补0）。exp=E+Bias=(-1)+7=6，exp表示为0110，注意根据位数往前补0。

综上，s是0（正数），exp是0110，frac是001，所以0.625的浮点数表示是0 0110 001。

例题2：十进制转换为浮点表示。将1.75转换为浮点数表示，s, exp, frac分别为1, 4, 3位。

0. Bias = 2^(4-1)-1=7。
1. 1.75 = $1.11_{(2)} \times 2^0$
2. M=1.11，E=0，E>1-7=-6，所以规格化表示。
3. frac表示为110（注意往后补0），exp=0+7=7，表示为0111。

综上，1.75 表示为 0 0111 110。

例题3：浮点表示转换为十进制。0 0111 110表示的数是多少？s, exp, frac分别为1, 4, 3位。

exp段是0111，不是全0、不是全1，所以是规格化。
M=$1.110_{(2)}$，
E=exp-Bias=7-7=0。
s=0。
所以表示的数 $V=(-1)^s \times M \times 2^E = (-1)^0 \times 1.11_{(2)} \times 2^0 = 1.11_{2}=1.75$

例题4：十进制转换为浮点表示。0.375表示成多少？s, exp, frac分别为1, 4, 3位。

0. Bias = 7。
1. 0.375 = $0.011_{(2)}$，图省事口算转换也可以想0.375 = 1/4 + 1/8，然后1/4和1/8对应的那两位为1。再转换成科学计数法就是$1.1 \times 2^{-2}$
2. M=1.1，E=-2，则frac为100，exp为E+Bias=5就是0101，故表示为 0 0101 100。

例题5：√-1表示成多少？

NaN，可以写0 1111 001之类的。

附录：对于上述s, exp, frac三个二进制段长度为1, 4, 3的非负数表格完整示例：

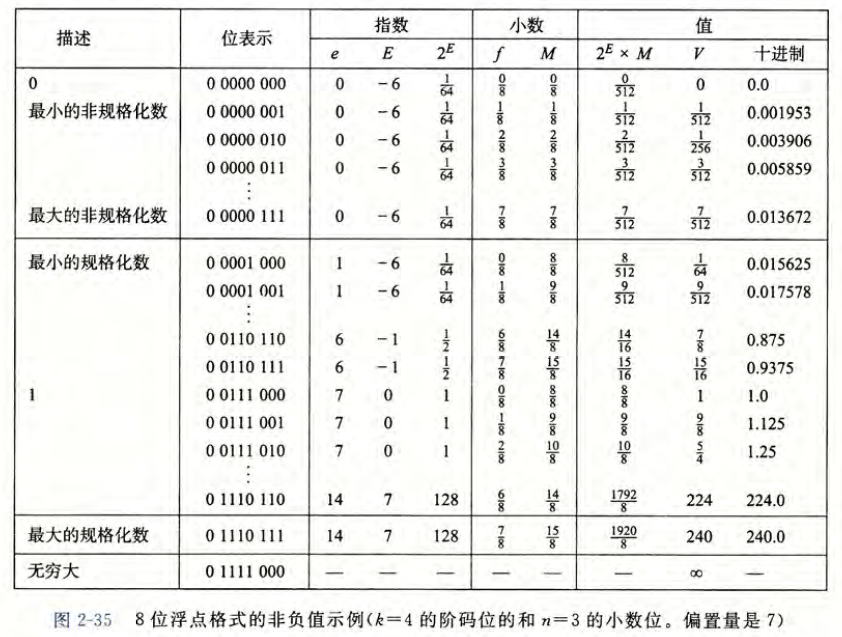
ps. 建议从上表格任选位表示和十进制，练习从十进制推位表示或从位表示推十进制，熟练掌握转换方法。